Help with RC high pass filter

[Tahoebrian5]

I'm having trouble understanding how to analyze the following RC circuit. I understand the basic condition but when it is a composite system not sure how to isolate each part. The bottom of the page is where I attempted to determine equivalent circuits. Please point me in the right direction

[Enzo]

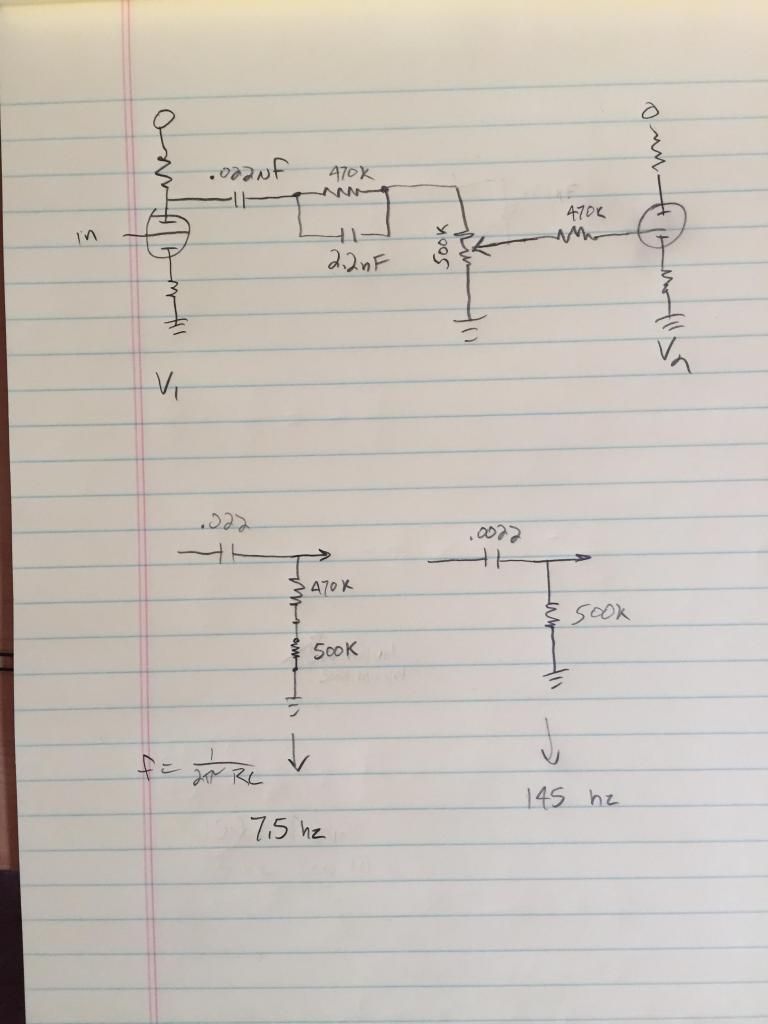
You ignored the 2,2 across the 470k. if you are interested, fine, but I never bother to calculate frequencies during repair work. But conceptually, think of it like this:

First, 470k and 500k are close so lets think of them as the same. Lower frequencies come from V1 through the 0.022 (are you sure all those caps are in nanofarads?) then the 470k and 500k form a voltage divider, 1/2, so half the signal level appears across the volume pot. At higher frequencies, the signal goes right through the 2.2 cap, thus bypassing the 470k. That means the higher freqs are not subject to the 1/2 voltage division. So the highs will be less diminished at the volume control. Thus the overall result is a brighter signal into V2.

[Tahoebrian5]

The first cap is in micro farads

So i think I get what your saying and it makes sense... So is my calculation correct? The freq's above 145hz are not subject to the divider? I guess Im having a hard time looking at caps and resistors in parallel and understanding how they interact.

[dwmorrin]

The freq's above 145hz are not subject to the divider?

First, note that you're calculating for the f=-3dB point with your RC formula. That means @ 145Hz the voltage will be attenuated -3dB, going through that filter.
Secondly, that exact calculation only applies when your input to the simplified RC network is a low impedance voltage source.
Since your actual voltage signal is coming off of a triode plate, you also have to consider the high source impedance if you want to get nitty gritty about it.

EDIT:
One way you can work through this is to just pick frequencies in say, decades (100Hz, 1k, 10k,) or whatever selection you like (octaves, etc) and just calculate reactances for the caps, simplify everything like resistors and do your voltage division.
Capacitors in this case are just frequency dependent resistors. Once you've picked a frequency, you can draw a resistor value instead for simple analysis.

[Tahoebrian5]

Can you elaborate on how the input source impedance can affect the filter? Everything I've studied so far for high pass talks about the capacitor interacting with the resistance to ground AFTER the cap in question. I've not seen anything that talks about the preceding resistances or impedance.

[dwmorrin]

Can you elaborate on how the input source impedance can affect the filter?

Sure, although let's call it "source impedance" or the "output impedance" of the source. "Input source impedance" is confusing for me.

It just means that ALL frequencies are coming "out" of the tube circuit with a series resistance that can be analyzed as the actual plate resistor in parallel with the plate resistance (plate resistance can be visualized as turning the plate-cathode path into a resistor). Since both B+ and ground are low impedance to AC, we take the two resistances in parallel.
More info here: Designing Common-Cathode Triode Amplifiers

Then will end up, for your average triode circuit, between 10k-100k. So you add a 50k resistor (or whatever you calculate output impedance to be) in series with the voltage source on your simplified circuit.

500k = 50k x 10, so it conforms to the rule that the input impedance is at least 10x the previous stage's output impedance so we can *mostly* ignore the output impedance effect, but you should add it to your analysis if you want spot on numbers.

Back to your RC filter analysis/simplifying questions:
Here's some good info on capacitive reactance: Capacitive reactance calculator reactance capacitor frequence - sengpielaudio Sengpiel Berlin

Note that the tricky part of reactance is that the power loss is more than the voltage loss. Check out the info in the link above to wrap your head around it. I just had to remind myself about all the details.

EDIT:
And to answer your question about filter schematics omitting the source impedance...
Simplified filter schematics always assume that the voltage source has an ideal 0Ω output impedance.
If you are driving your filter from the output of an op amp, then you have pretty close to this ideal output impedance.
Otherwise, you must add your real world impedance/resistance as a series resistor between the voltage source and the filter input.

[R.G.]

The lecture on "Thevenin-Norton equivalents" is usually the next one after "series-parallel combinations".

"Thevenin norton equivalent circuit" would be a great search term to type into google.

[J M Fahey]

Agree.
Saying the same in a very simplified way:

a) to analyze low frequency cutoff you used .022uF in series with 470k + 500k which is .022uF in series with 1M .
Fine.

b) but there is an unseen series resistance/impedance in that circuit which is very real and affects calculations yet you didn't draw

Fact is audio signal in the real world (such as inside a tube guitar preamp) is not coming straight from a Lab type signal generator (more on that later) or an Op Amp which have essentially 0 or very low internal impedance but from an earlier tube stage, which as calculated above is roughly 50k .

Then you should add a 50k resistor to the left of the .022uF cap.

And since they are in series, it's the same if it's on the left of the cap, or on the right, so your network is really .022uF in series with 50k+1M = 1050K , 5% higher , so real cutoff frequency is 5% lower than expected.

No big deal ?

Well, not much in this case, because it's an "easy" load to drive ... and even so another problem starts to appear:

no big deal in calculating low frequency cutoff but when you calculate the "treble boost" gained bypassing the 470k resistor by the .0022uF cap , we assume that at high frequencies it will eventually get down to 0 ohms so attenuation will be , let's see:
0 ohms in series with 500k pot= no attenuation ...

or to see it another way, you should get "6dB boost" compared to that network 6dB attenuation ...

but this is not true any more, those unseen 50k are throwing that away by 10% or about 1dB.

And this is a very simple circuit.

In the case of a tone control, which is more complex to study, it has variable resistors (the pots) inside, at certain frequencies it has lower than expected impedance, and those series 50k throw calculations out of whack.

That's why Black/Silverface Fender controls , which use 250k pots and are driven from 12AX7 plates do not behave as calculated and are so "interactive"
Which is a fine way to say that they are so poorly driven that moving any pot varies the effect of others which are untouched

So Tweed/Marshall controls added a "useless"? 0 gain cathode follower to the tone stack driver.

Why?
Because it lowers impedance to a much lower value, less than 5k, so now tone controls are much more accurate, mainly rising treble does not cut bass.

So when in a Fender you rise highs, simultaneously you cut bass, like it or not, amp becomes good for , say, twangy Country, Strats and Teles love it.
No surprise here.

And in a Marshall Bass stays as strong as before, good for thick Heavy Metal.
And Treble "boosts more" so you get more aggressive highs, also good for Metal.
And Humbuckers love it.
No surprise either.

So in a nutshell "unseen" internal impedance does play a big role.

So much so, that in MB Maverick amps there is a "Bright/Fat" switch which most who analyze it despise as useless/crazy.
It's between V1a and tone stack, you can go either straight or through cathode follower V1b:



Hey !!!! cathode followers are FLAT !!!!!!
Yup.

So it should not give you a fatter sound !!!!!!!

Think again.

The cathode follower is flat indeed ... but the tone controls behave different.

Classic killer amps are full of such "unseen" little details, most time tested by ear by countless Musicians, and which are not readily apparent.

That's why I so strongly dislike many "Internet mods" of the type: "I love VOX chime but I will enlarge such and such caps so it has more body, as a Marshall which I also like" or "I find this amp icepicky (in my bedroom) so I will clip bright caps off" , etc.

All you get is butcher original sound and gain very little, if any at all, of what was expected.

In fact, in a Pro Tech Forum I also visit, the following dialogue is often reported:
- "hey !!! amp now sounds killer !!!! what did you do to it"?
- "I just pulled out Mods and returned it to Factory specs" !!!!!!!!!!!!!!!

Not kidding.

[Tahoebrian5]

So my calculations are not correct? Joking

Thx for the thoughts. I've got a bunch of topics to look into.

I'm starting to so just how finicky tone circuits are.

[Dave H]

So my calculations are not correct?

Your calculations are fine. To get an idea of the frequency response first consider the case when the frequency is high (> 10 x 145Hz) the 0.0022u is effectively a short circuit compared to the 470k so the 'gain' from first stage to vol pot cw is 1 (0dB). Now consider a frequency one tenth of 145Hz, the 0.0022u is open circuit compared to 470k so the 'gain' is 0.5 (-6dB) because of the 470k, 500k potential divider.

We can use the above information to roughly plot the frequency response curve. Starting at 10kHz say, the curve will be flat at 0dB down to 1450Hz then it will slope down to the -3dB point you calculated at 145Hz then it will try to slope down to -6dB at 14.5Hz but the 7.5Hz -3dB point starts to take effect making it -9dB at 7.5Hz and below that it will slope down at a rate of -6dB per octave because of the 0.022u and 1M resistance.

This only gives a rough idea of the frequency response. To calculate it accurately you'd need to resort to complex numbers to allow for the phase shift. The -3dB points you calculated where the resistance R = Xc of the capacitor are -3dB (0.707) and not -6dB (0.5) because the phase shift at this point is 45deg.

Edit - Here's a simulation

[Tahoebrian5]

I was just starting to think I was getting a handle on this and now there is phase shifts to account for?! So are you saying the phase shift is different for each capacitor so that causes some havoc in some way?

Just to make sure I fully have calculating roll off points correctly in my head, so ALL resistances must be plugged into the equation from source to ground? In the case of tube stages the preceding stage would be the source I suppose. What about a guitar? I know the capacitance of a cable goes into play but is there a source resistance built into the pickup as well as the vol control? The pickup being equiv to a voltage source and a resistor?

[dwmorrin]

I was just starting to think I was getting a handle on this and now there is phase shifts to account for?! So are you saying the phase shift is different for each capacitor so that causes some havoc in some way?

The phase shift effect refers to the voltage and the current coming and going at different rates defined by physics. Capacitors and inductors have opposite behavior this way.
You won't need to think much about it because your f[-3dB]=1/(2πRC) formula is already taking this into account by specifying -3dB (70%) instead of -6dB (50%).

What about a guitar? I know the capacitance of a cable goes into play but is there a source resistance built into the pickup as well as the vol control? The pickup being equiv to a voltage source and a resistor?

I'm sure there are MANY threads about this within MEF and other forums that cover this many times over.

The pickup is a long wire wrapped many times about a magnet and it works off of the principles of induction. So, your ideal voltage source that is "magically" coming from the strings needs to be in series with a resistance representing the actual dc resistance of the wire (usually in the ballpark of 3-6k or so...) in series with a fairly large (1-10H?) inductor, and in parallel with not only cable capacitance but any capacitance between pickup windings as well. The main thing is the high value inductor. This creates a natural low pass filter effect. You'll find the output impedance of guitar pickup shoots up towards infinity as you increase the frequency.

[Mick Bailey]

For my own purposes I find it easy to set the circuit up in PSpice and do an AC sweep analysis. You can also sweep the pot rotation in decade increments. You can then play around with values and source/load impedances. I find having a visual plot of the sweep much more useful than figures on paper.

[J M Fahey]

I was just starting to think I was getting a handle on this and now there is phase shifts to account for?! So are you saying the phase shift is different for each capacitor so that causes some havoc in some way?

True but don't overthink it.
A simplified rule of thumb that works is:

a) consider capacitors (and inductors) as simple resistors, IF you are away from the nominal crossover frequency.
b) at or very near the crossover frequency, attenuation/boost is 3 dB instead of expected 6dB.

this simple solution goes a long way

Just to make sure I fully have calculating roll off points correctly in my head, so ALL resistances must be plugged into the equation from source to ground?

Basically yes, but you can ignore very small ones in series or very large ones in parallel.
5%/10% precision is usually enough, in some places even 20% (what was standard in Leo's time, go figure) ; as Enzo often says, "it's not NASA or rocket Science".

In the case of tube stages the preceding stage would be the source I suppose. What about a guitar? I know the capacitance of a cable goes into play but is there a source resistance built into the pickup as well as the vol control?

Yes.

The pickup being equiv to a voltage source and a resistor?

Pickups?
MUCH worse: a pickup is a generator plus a series resistor plus a series inductor, which to boot is so large that it can not be ignored.

[J M Fahey]

From the VERY good site BuildYourGuitar.com :: The Secrets of Electric Guitar Pickups which I recommend you read:

The Pickup as Circuit

From an electrical standpoint, a magnetic guitar pickup is equivalent to the circuit in Fig. 1.



Fig. 2. A pickup as an audio voltage source plus second-order lowpass

The external load consists of resistance (the volume and tone potentiometer in the guitar, and any resistance to ground at the amplifier input) and capacitance (due to the capacitance between the hot lead and shield in the guitar cable). The cable capacitance is significant and must not be neglected. This arrangement of passive components forms a so-called second-order low-pass filter (Fig. 3).


Fig. 3. A pickup plus real external load (pots, cable, and amp input resistance)

Fig. 14 shows the frequency response of a 1972 Fender Stratocaster Pickup with constant capacitive load (470 pF) and eight different Ohmic loads from 10 kOhms to 10 MOhms. It can be seen how different values of pots in the guitar influence the height of the resonance peak. With 47 kOhms or less the peak vanishes.

Won't even speak of what happens when we add a simple (1 pot 1 cap ) tone control to the guitar.
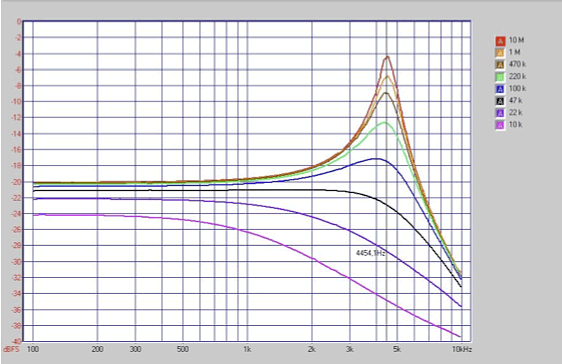
Just a free sample :