Questions revolving one tube reverb circuit

[überfuzz]

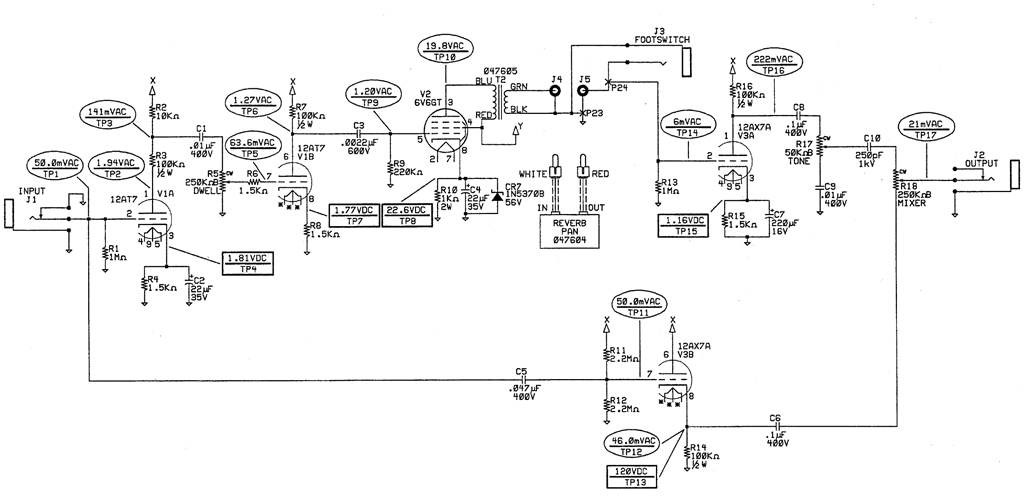
How much the tank shakes the springs depends on how much AC current is flowing through the input coil. We would prefer that the springs shake the same at all of the frequencies that concern us, so we want constant current for those frequencies. In order to get constant current from your driver, the load presented by the coil circuit must be constant. This isn't going to happen with just a capacitor and a coil.

The impedance of a capacitor changes with frequency and so does a coil. The total impedance of a capacitor and a coil in series is the absolute value of the difference of the two impedance values at any given frequency. At low frequencies, the capacitor has a high impedance and the coil has a low impedance so that the total impedance is approximately the capacitor impedance. At high frequencies, the capacitor has a low impedance and the coil has a high impedance so that the total impedance is approximately the coil impedance.

In between the two impedance extremes the impedance drops. When the impedance of the capacitor equals the impedance of the coil, the theoretical impedance drops to zero. In practice there is still some impedance, but it is very low. This brings up the first problem with the 0.1uf capacitor. With a 4F tank, the very low impedance occurs at just over 1KHz. At and around this frequency the signal gets an ugly clip and the reverb sound is undesirable.

The second problem with a 0.1uf capacitor is that the higher impedance at lower frequencies causes less current to flow through the coil than at mid and high frequencies.

If you add a resistor between the capacitor and the coil, you have a series LRC circuit. The total impedance of this is the square root of the sum of the squared value of the resistor and the squared value of the total impedance of the capacitor in series with the coil. Obviously, if we make R very large, the total impedance is approximately R and all of the problems with a 0.1uf capacitor go away. The current will be constant, but there won't be much of it. So we hit the calculator to find an R that is much lower but that still gives us an acceptable range of total impedances at the frequencies that concern us.

After a few strokes on the calculator, the 0.1uf problem reappears. The high impedance at lower frequencies forces us to use an R that is higher than what we want. So we raise the value of the capacitor to decrease the impedance at lower frequencies. I don't want to use a huge electrolytic here because they are expensive at that voltage and they are bulky. I want the smallest one that causes the LRC equation to come out close to what I want.

So it is all a balancing act and 1.0uf, 3Kohms, and a 0.235H coil is acceptable to me.

Okay, thanks! Sounds legit. :-)

I think I'll go for the tank I presented above, 9GB2C1B. The impedance of that tank is easier to match with a ECC82 stage.

[Gregg]

Yes, it´s basically that, but I suggest you do not reinvent the wheel, there´s already 3 or 4 versions of them, all solidly established, just pick one that suits you.
No need to design starting with a blank sheet of paper.

+1. Completely agree.
How come every once in a while a long time discussed and established topic will pop up and trigger lengthy theoretical discussions like every moment the wheel will be discovered only to arrive at the same conclusions again and again.
Please start staring (not looking) at schematics! As many as possible and for as long as possible!
If you think that you will arrive at some magic unknown solution in this field I have to break you the bad news but it's not happening.
Take something well known and include it in your design.
By the way even a single 12AX7 reverb doesn't sound bad but it also depends who you're asking.

P.S. I don't know if the forum platform allows it but maybe there should be some sticky topics including this one.

[Enzo]

Oh we have stickies, but after a while the whole page is stickies, and I think the majority of users ignore the stickies, hell most of them don't use the search feature. For that matter too many don;t even use google.

[66 Kicks]

Yes I do, but I'm lazy, I use a spread sheet I found on the net. Why?

Using the 12AU7 anode current vs anode voltage @ grid voltages set of curves, draw a DC load line using an HT of 350V and a plate resistor of 22K. Now find the bias points for a 270r cathode resistor and a 560r cathode resistor. For the AC load line, use the worst case scenario of 3K for the reverb load that is in parallel with the 22K. Draw an AC load line through both bias points. Now you can see that the 560r setup can swing more current before clipping than the 270r setup. You can also see that 560r is about as high as you can go without exceeding the 2.75W maximum dissipation (if you care about that sort of thing).

[Chuck H]

How come every once in a while a long time discussed and established topic will pop up and trigger lengthy theoretical discussions like every moment the wheel will be discovered only to arrive at the same conclusions again and again.
Please start staring (not looking) at schematics! As many as possible and for as long as possible!
If you think that you will arrive at some magic unknown solution in this field I have to break you the bad news but it's not happening.

Man! Really? That's just, straight up, a short cut to thinking. I design one off customs sometimes. I've run up against problems that, at face value, should have been solved by just kludging some known circuit or approach into my design, but it just wasn't as good as I thought it should be for one reason or another. I don't have 66 Kick's electronic chops, but I've often had to find a previously unexplored (for guitar amps anyway) circuit/design to get the performance I wanted. This forum has been instrumental.

For me, that's the point of the forum. It's a place to discuss circuits, improvements, problems and creative solutions. Not just an archive or "how to" instructional. Some of us may be getting long in the tooth, but I never felt a "Good enough for Grandpa, good enough for me." vibe here before. The implication that it's impossible to improve on what's gone before seems extremely short sighted to me.

I read an article where the inner workings of the early Fender operation were discussed. It was said that an inside "joke" slogan was "We don't make them like we use to. And we never did." You don't get there just doing what someone else did.

[J M Fahey]

Agree on deep designing on a full amp, possible variations are mind numbing , but on reverb drive and recovery there´s just 3 or 4 variations:

* full power amp, pentode output, 2 to 5 W available, plus recovery and full set of controls (dwell, tone, reverb mix/intensity) as in Fender external reverb.

* simplified version of same: single or dual triode driving, single control, can go from excellent : full 12AT7 driving, 1 or 2 W RMS available , to meh, an unsuitable-as-power-amp 1/2 12AX7, probably a few hundred mW, used by many, showing bean counters have an influence even on supposedly boutique class amps, including Mesa Boogie.

The B52 head we discussed short ago had a single tube reverb, but at least used good balance between drive and gain capabilities 12AT7.

* Transformerless type: saves $$$$$ but uses very inefficient power transfer system: drives a quite low value plate resistor, think Ampeg or Traynor, ideally same impedance as tank input which would be 25% efficient (ideal case) or higher mismatched value, where power generated is low and power transfer is abysmal, only a few mW available.

Situation would be improved IF an inductor were used as a plate load, because all DC would go through it, all AC towards the tank, but I guess it won´t happen today.

What plate resistor values are used to have some hope of driving a tank?

* Ampeg: 6CG7 triode driving 10k 5W + .47uF

* Traynor: 15k 10W on the plate of a ... 6BQ5 ; 10uF coupling cap ..... maybe he was on to something

with due respect, not so sure how far away from some of these 2 basic solutions (transformer or transformerless) can we go.

Just a personal suggestion, I would use it but purists will probably object: standard triode (think 12AX7), driving a current gain only pair of complementary transistor buffers, fed from their own more reasonable suppy.

A 12AX7 triode can provide some 1 or 2 mA reasonably, a 12AU7 maybe 10/12 mA, the hybrid I suggest woud have all the gain and sensitivity of 12AX7 and the current capability of transistors.

But of course it would be Heresy

[Ken Moon]

Check out the reverb circuit in this Vibro-King.
EL84 driver and 12AX7 for recovery.
If you want to go one-tube, you could use an ECL86 (and maybe a 6GW8).
The Vibro-King has a beautiful lush reverb sound.
Notice how early in the circuit the reverb is located (after the first gain stage).

Here is the reissue '63 Fender standalone reverb. It uses a 6V6 driver (original used 6K6) and 12AX7 recovery.

Both of these choices have Dwell, Tone and Mix controls, which give a wider range of tones from the reverb circuit.

[Justin Thomas]

I would think they were trying to capture the magic of ahving a Reverberate Unit as close to the front of the amp as possible, like the "good old days" maybe. This was probably my favorite of the Custom Shop amps that I had a chance to play...

Despite the above comments bout Ampeg's cap reverberate, I usually found them to be WAY more than any Fender. Despite maybe being low current, the effect is often way too much for anything besides slow jazz. The depth of the effect put my Dual Showman Reverberate through its paces, which was my other favorote Reverberate ever... I never had to turn it past 12. I am speaking of the mid-60s Ampegs here, not the 70s amps...

If you kick your amp hard and it doesn't make a heinously loud racket, the Verb isn't storing enough! And agree on the Mesa verbs being effectively useless!

Justin

[pdf64]

...* Transformerless type: saves $$$$$ but uses very inefficient power transfer system: drives a quite low value plate resistor, think Ampeg or Traynor, ideally same impedance as tank input which would be 25% efficient (ideal case) or higher mismatched value, where power generated is low and power transfer is abysmal, only a few mW available.

Situation would be improved IF an inductor were used as a plate load, because all DC would go through it, all AC towards the tank, but I guess it won´t happen today...

How about using a high voltage current source, eg based around a MOSFET, for the plate dc operating point, instead of an inductor / resistor?

For regular home builders, a barrier to using full-on silicon circuits for reverb etc may be the extra power supply/s needed.
But if a silicon device or 2 can be incorporated into a tube stage to give things a helping hand, then it may become more tempting.

[g1]

There were some hi-fi units that drove 600 or 800 ohm speakers OTL. Philips?
Not sure which power tube was used, but why not directly drive a higher Z tank like that?

[nickb]

How about using a high voltage current source, eg based around a MOSFET, for the plate dc operating point, instead of an inductor / resistor?

For regular home builders, a barrier to using full-on silicon circuits for reverb etc may be the extra power supply/s needed.
But if a silicon device or 2 can be incorporated into a tube stage to give things a helping hand, then it may become more tempting.

Here's a suggestion.

With a 12AU7 the Mu is low and so not very suitable for the recovery stage. On the other hand a 12AX7 doesn't make a good driver.

You can turn it into a nice current driver with a $0.60 sillicootie and not need extra power supplies if you do this (below). I used a ubiquitous 8EB2C1B for the tank. The drive current is about 5mA for 1V in. The recommended drive is 3mA but know it can take a lot more than that and the more the better up to a point. I rolled off the LF a little since I don't think it sounds great in a reverb. You might want to roll off some more. Also the HF above 10KHz as it is not needed and you have to control the Vpp at the collector as frequency goes up.

Hopefully it's obvious that you need to replace the voltage generator on the input with a 470K grid leak and add an AC coupling cap.

[jimboyogi]

* Transformerless type: saves $$$$$ but uses very inefficient power transfer system: drives a quite low value plate resistor, think Ampeg or Traynor, ideally same impedance as tank input which would be 25% efficient (ideal case) or higher mismatched value, where power generated is low and power transfer is abysmal, only a few mW available.

Situation would be improved IF an inductor were used as a plate load, because all DC would go through it, all AC towards the tank, but I guess it won´t happen today.

What plate resistor values are used to have some hope of driving a tank?

* Ampeg: 6CG7 triode driving 10k 5W + .47uF

* Traynor: 15k 10W on the plate of a ... 6BQ5 ; 10uF coupling cap ..... maybe he was on to something

with due respect, not so sure how far away from some of these 2 basic solutions (transformer or transformerless) can we go.

Great summary! I'm curious about the inductor as plate load idea, but also E-theory challenged. For an inductor with DCR of 15K as plate load of a 12AU7 triode, what other specs would it need?

[uneumann]

Check out the reverb circuit in this Vibro-King.
...
Both of these choices have Dwell, Tone and Mix controls, which give a wider range of tones from the reverb circuit.

Just my 2-cents -- I've come to appreciate the unity-gain mixing scheme in these circuits with the follower driving the "dry" end of the mix pot. Avoids using big 3M resistors and gain loss. You can insert reverb into an existing circuit without impacting the gain/levels of the existing amp dry signal. You're only adding reverb to it.

[überfuzz]

All who dished ideas and pointers - Thank you very much! :-)

[Erased stuff written under influence of firewater.]

[Enzo]

Physics doesn't lie, but it only answers the questions you ask it. If you ask it to have XYZ response, it will tell you, but that won't make XYZ response a suitable guitar tone. Those already-invented wheels have in their process already overcome the shortfall of the basic design theory.