Can you double check my results?
I'm calculating the halfboost frequency for a given cathode bypass capacitor value in an output stage. Most of the discussions seem to center around implementation in a preamp stage. In order to achieve accurate results, I'm using this formula:
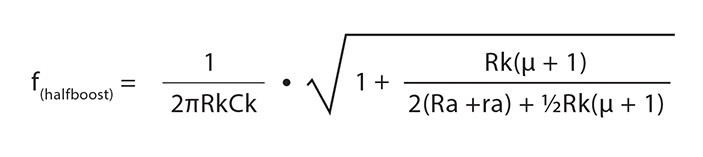
*
The formula was found in this short article:
http://valvewizard.co.uk/ChoosingBypassCaps.pdf
Here is the datasheet for an EL84:
EL84-2.pdf
*
the parameters for a pair of EL84s operating in a class AB push-pull output stage are as follows:
10k p-p load impedance
220Ω Rk(per tube)
20µF Ck(per Rk)
internal resistance ≈ 38k
µ = 19
solving for f during class B operation I came up with f(halfboost) ≈ 37Hz (37.125908162)
Is this correct?
I'm calculating the halfboost frequency for a given cathode bypass capacitor value in an output stage. Most of the discussions seem to center around implementation in a preamp stage. In order to achieve accurate results, I'm using this formula:
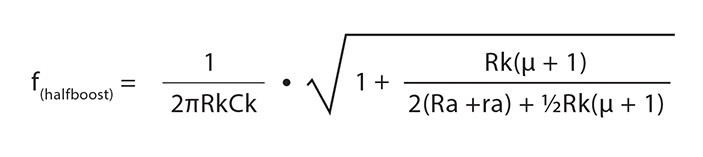
*
The formula was found in this short article:
http://valvewizard.co.uk/ChoosingBypassCaps.pdf
Here is the datasheet for an EL84:
EL84-2.pdf
*
the parameters for a pair of EL84s operating in a class AB push-pull output stage are as follows:
10k p-p load impedance
220Ω Rk(per tube)
20µF Ck(per Rk)
internal resistance ≈ 38k
µ = 19
solving for f during class B operation I came up with f(halfboost) ≈ 37Hz (37.125908162)
Is this correct?
Comment