seires / parallel wattage question

[Randall]

If it is my original question some are unsure of, I apologise if I was unclear. I know a 100 watt resistor is a 100 watt resistor all day, that seems obvious enough. I was thinking in terms of dummy loads as well as speakers in cabinet combinations. I am looking at building a dummy load array, and wanted to know what the power handling ability would be for the different series/parallel pairings of 100 watt resistors. Also, was wondering about the series/parallel wiring in a 16 ohm Marshall cab loaded with four 16 ohm 25 watt greenbacks connected to a 100 watt Marshall head. By the look of RG's answer, whether wired in series or parallel, those four 25 watters are handling 25 watts each for a total of 100 watts. Right?

[The Dude]

Assuming they are the same value, yes. You can figure this out using ohms law if they are not the same value.

[SoulFetish]

Randall, if I could add a bit to what has been already been explained about the total power of series/parallel resistor combinations. It probably goes without saying, but you can only add the total power ratings of each resistor if the all the values are the same.
But need to make a total load resistance using different value series or parallel resistors, you can still figure the each current, voltage, and combined power rating pretty easily. One of the things which I which cleared up a lot of circuit questions I had was when I learned Kirchhoff's voltage and current laws. It was kind of like a lightbulb moment. Using Kirchhoff's and Ohm's laws, you can figure out pretty much any network of resistances. Hopefully this makes some sense and you find it helpful.
I really like how Morgan Jones explains it in "Valve Amplifiers", so I'll paraphrase.

Kirchhoff's Voltage Law states:
The algebraic sum of the EMFs (or sources of electrical energy) and potential differences(voltages dropped) acting around any loop is equal to zero.
Another way of saying that using your series resistor question is: If you have two load resistors in series connected to the secondary of an output transformer, the sum of the voltages dropped across each resistor must be equal to the total voltage measured across the output transformer leads. See fig A. (the voltage and current figures might seem like random choices, but they aren't and will hopefully make sense later)

Kirchhoff's Current Law states:
The algebraic sum of the currents flowing into, and out of, a node is equal to zero.
Another way of saying that using your parallel resistor question is: If you have two load resistors connected in parallel to the secondary of an output transformer, the total current flowing into the junction of the two resistors, must be equal to the sum of currents flowing out of each resistor. Or any current flowing into the point where any resistors are connected (the node), will be split off and shared by some ratio between the resistors. But, the all the currents flowing in each resistor added together must be equal to the current flowing into the node they are connect together. See fig B.


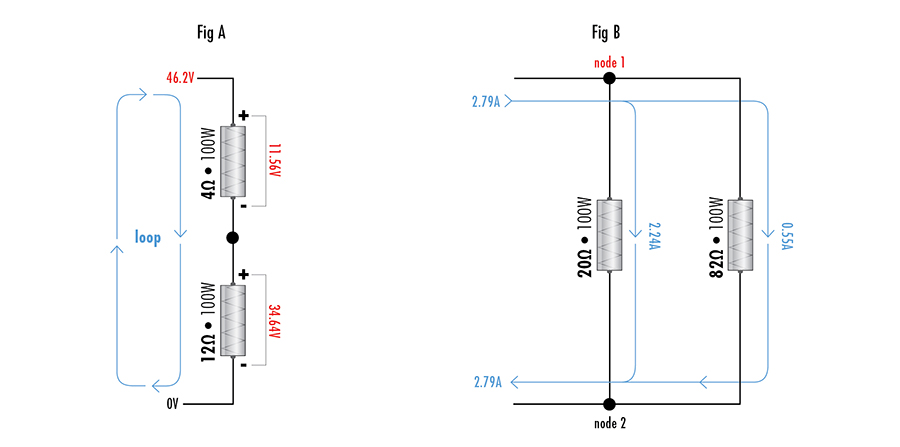
So, what does that have to do with the power handling of resistors? Bare with me...
Lets, keep it simple and assume two resistor combinations. According to Kirchhoff's laws above, we can see that any network of resistors is going to share one of the components of the power equation: voltage or current. If the resistors are connected in series, they will have the same amount of current flowing through them, and split the total voltage between them - think the voltage divider rule.
Or, if they are connected in parallel, they will have the same voltage drop across them, and split the total current between the two resistors.
As long as the resistors are the same value, all voltages and currents are split evenly. So, if both resistors are rated for 100W the total power handling of the two resistors combined can be doubled since the total power will be shared evenly.
But what happens if you have need to use the two different value resistors to get the total resistance you're looking for? We can use Kirchhoff's and Ohm's laws to figure it all out.
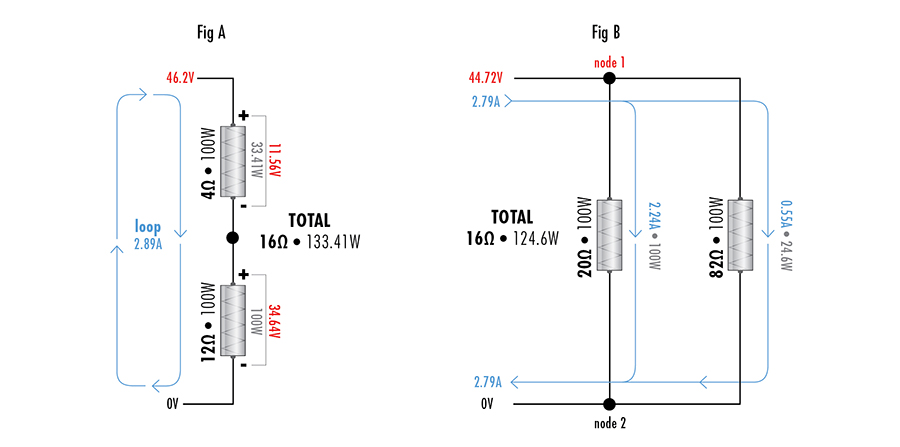
Lets say you need a total load resistance of 16Ω. You have a series combination, and a parallel combination of two resistors, each combination equaling 16Ω. All resistors are rated for 100W, but your series combination is made up of 12Ω and 4Ω resistors, and your parallel combination is made up of 20Ω and 82Ω resistors. You can't just double the power handling of the two 100W resistors because they don't share the power equally. In the series combo, they both have the same current in each resistor, but the 12Ω resistor has a higher voltage, meaning the 12Ω resistor will reach it's max 100W power dissipation(voltage*current) before the 4Ω resistor will. In the case of the parallel combination, the voltage drop will always be the same between the two resistors, but we know from Ohm's law that the current through the 20Ω resistor will always be higher than the 82Ω resistor. So, the 20Ω resistor will reach it's max 100W dissipation before the 82Ω resistor. Check out the illustration below.
How do we determine the power handling of each of our 16Ω combinations then? Stay tuned because I'm running out of steam here
(Maybe I can tag someone else in here who can talk about the power law equations or correct me if I've made an error. I haven't double checked anything yet)

[R.G.]

If it is my original question some are unsure of, I apologise if I was unclear. I know a 100 watt resistor is a 100 watt resistor all day, that seems obvious enough. I was thinking in terms of dummy loads as well as speakers in cabinet combinations. I am looking at building a dummy load array, and wanted to know what the power handling ability would be for the different series/parallel pairings of 100 watt resistors. Also, was wondering about the series/parallel wiring in a 16 ohm Marshall cab loaded with four 16 ohm 25 watt greenbacks connected to a 100 watt Marshall head. By the look of RG's answer, whether wired in series or parallel, those four 25 watters are handling 25 watts each for a total of 100 watts. Right?

Right.

For resistors, the power P dissipated in the resistor is P = V²/R and also P = I² * R. These are equivalent statements because in all cases P = V * I and for a resistor, V = I * R.

We know that for parallel resistors, the voltage across the resistors is equal, so the power in each resistor is P = V²/R independently, so in a parallel combination of resistors of any values, each resistor is heated proportionately to one divided by the resistance. An 8 ohm resistor in parallel with a 4 ohm resistor will dissipate half of the power that the 4 ohm does for all values of applied voltage.

Likewise, resistors in series will have exactly the same current through them, so in series, resistors will dissipate power in direct proportion to their resistance. An 8 ohm resistor in series with a 4 ohm resistor will dissipate twice the power of the 4 ohm.

I had to take circuits classes where the homework involved answering questions on exactly this kind of thing: given a network of various series and parallel combinations of resistors and a battery, what is the voltage and current in each resistor? The answer could be arrived at by two paths. One was to write the set of loop and node equations, then solve the set of simultaneous equations; this was the answer that was what the profs really wanted. The other path was to start reducing the network to a single resistance by computing the various values of resistors in parallel and series, getting the current in the equivalent resistance, and then back-computing the current and voltage in each resistor. With a little practice, you can do this second way largely in your head, no paper needed. The answer you gave the professor depended on the professor. If they had purely academic background, they'd ding you good for not using the loop/mesh equations. The ones who'd been in industry and retreated would recognize the value of the equivalent-networks approach and give you extra credit.

In speaker networks, you're only dealing with three or four values of "resistance"; four, eight, sixteen, and maybe two if you have a perverse amplifier/cab. This makes speaker loading calculations a breeze. Two eight ohm resistors in series gives you a sixteen, two in parallel gives you a four. Two eights in parallel experience the same voltage across them, so they will have equal power dissipated no matter what the voltage. Two eights in series divide the voltage between them, but have identical currents, so they will dissipate equal power because they have equal currents.

For a cab with four eight ohm speakers, you can string them all in parallel, for two ohms; the power rating is then four times the power for each speaker. Well, if they're not identical power ratings, it's four times the lowest power rating, because while the power >dissipated< is equal, the low-rated on will burn up first as it exceeds its power >rating<.

You can hook all four up in series, and get thirty two ohms. The power rating is equal to four times the individual rating because they all have the same current in them.

If you hook up two of the eights in parallel, you get an equivalent four ohms, and the power dissipated is twice the power of each eivht ohm resistor.

If you hook up two of the eights in parallel for four ohms, then put this in series with another pair of parallel eight, you get back eight ohms, but with all four eight-ohms sharing the power, the power rating is four times the power of the eight ohm resistors.

The question really reduces down to findng out how many resistors you can bring to bear. In a load box with only four resistors of eight ohms each, you can get two ohms at four times the power of one resistor; four ohms at >two< times the power of one resistor because you can only make four ohms using two resistors; eight ohms with four times the power of one resistor; sixteen ohms at two times the power of one resistor; and thirty two ohms at four times the power of one resistor.

It all depends on how many resistors you can get to share the load.


Here's a question they used to try to spring on us: Say you have FIVE eight ohm resistors, all the same value. You hook a up two of them in series to a battery. It's simple to compute the voltage, current, and power in both resistors. Now you use two more, and make them another series string, and hook that in parallel to the battery. Again, it's easy to compute the power in each resistor.

But now you take the fifth resistor, and hook it between the middle points of the two series strings of resistors, making an "H" shaped network of resistors across the battery. What's the power in that middle resistor?

[nickb]

If it is my original question some are unsure of, I apologise if I was unclear. I know a 100 watt resistor is a 100 watt resistor all day, that seems obvious enough. I was thinking in terms of dummy loads as well as speakers in cabinet combinations. I am looking at building a dummy load array, and wanted to know what the power handling ability would be for the different series/parallel pairings of 100 watt resistors. Also, was wondering about the series/parallel wiring in a 16 ohm Marshall cab loaded with four 16 ohm 25 watt greenbacks connected to a 100 watt Marshall head. By the look of RG's answer, whether wired in series or parallel, those four 25 watters are handling 25 watts each for a total of 100 watts. Right?

Ah, you want a dummy load, huh?...

Here's mine. I have two of these with the resistors mounted under a aluminum chassis. The top of the chassis has a very large heatsink (from an old Mackie SRM450) and fan on the top. Does 2 - 16 ohms, two channels max 800W @ 2 ohms per channel.

Dummy Load.pdf

[R.G.]

Forgot: if you want a high power load, go to Goodwill and buy a few hairdryers. Take them home, take them apart, and measure off lengths of the resistance wire that are 8 ohms long.

[Helmholtz]

Forgot: if you want a high power load, go to Goodwill and buy a few hairdryers. Take them home, take them apart, and measure off lengths of the resistance wire that are 8 ohms long.

What about increasing resistance with power/wire temperature?

[SoulFetish]

What about increasing resistance with power/wire temperature?

You could take a measurement of the room temperature resistance and measure the increasing resistance by measuring the voltage/current relationship at intervals as you increase the voltage across the load and plot the curve. Or, you might be able to calculate it looking manufacturing data of nichrome wire. Correct?

[R.G.]

All metals have some change in resistance with changes in temperature, the temperature coefficient of resistance.

The exact values for each metal depends on conditions, alloy, phase of the moon, and so on. I always go look up the numbers when I need them. These numbers came from here: https://www.allaboutcircuits.com/tex...t-resistance/]

For copper, it's +0.4% (about) per degree C. So if you heat copper wire by 10C, its resistance increases by 4%. Nichrome has a significantly smaller tempco than copper, about +0.00017 (0.017%/C), or about one twenty-third of copper's change per degree.

So a nichrome heating element will be about 23 times as stable per degree C rise as copper wire. There are a lot of asterisks and gotchas in that view of things, as copper has a lot lower resistivity, so you'd need either much thinner copper wire or much longer copper wire as nichrome to get the same resistance, and so it would transmit heat to air differently, making comparisons between copper and apples more difficult.

Most things transfer heat to air roughly by the fourth power of the temperature difference IIRC (and I ought to go look that up, too) between the material and the air, so there's a compression effect of more heat getting out as the temp difference with air gets bigger.

Nichrome is used for glows-red heating elements because it's stable at high temps. In a speaker emulator, if you used the typical thickness of nichrome in a hair dryer, it would not be changing temp nearly as much as in the hair dryer it came from. These devices tend to be about 1kW on high setting, that being about all you can reliably get out of a 15A socket.

Hmmm. Here's a thought. For 120Vrms and 8 ohms, the power is about 120*120/8 = 1800W. So if your amp can put out 1kW+, a hair dryer or toaster makes a modestly good dummy load as is.

[Dave H]

Here's a question they used to try to spring on us: Say you have FIVE eight ohm resistors, all the same value. You hook a up two of them in series to a battery. It's simple to compute the voltage, current, and power in both resistors. Now you use two more, and make them another series string, and hook that in parallel to the battery. Again, it's easy to compute the power in each resistor.

But now you take the fifth resistor, and hook it between the middle points of the two series strings of resistors, making an "H" shaped network of resistors across the battery. What's the power in that middle resistor?

Is this a trick question?
You are adding the fifth resistor between two points of equal voltage so it has no power.

[SoulFetish]

Is this a trick question?
You are adding the fifth resistor between two points of equal voltage so it has no power.

Oh, right. Otherwise, we would need to know the battery voltage... which was omitted on PURPOSE!
Very sneaky. Very sneaky indeed.

[Helmholtz]

All metals have some change in resistance with changes in temperature, the temperature coefficient of resistance.

The exact values for each metal depends on conditions, alloy, phase of the moon, and so on. I always go look up the numbers when I need them. These numbers came from here: https://www.allaboutcircuits.com/tex...t-resistance/]

For copper, it's +0.4% (about) per degree C. So if you heat copper wire by 10C, its resistance increases by 4%. Nichrome has a significantly smaller tempco than copper, about +0.00017 (0.017%/C), or about one twenty-third of copper's change per degree.

So a nichrome heating element will be about 23 times as stable per degree C rise as copper wire. There are a lot of asterisks and gotchas in that view of things, as copper has a lot lower resistivity, so you'd need either much thinner copper wire or much longer copper wire as nichrome to get the same resistance, and so it would transmit heat to air differently, making comparisons between copper and apples more difficult.

Most things transfer heat to air roughly by the fourth power of the temperature difference IIRC (and I ought to go look that up, too) between the material and the air, so there's a compression effect of more heat getting out as the temp difference with air gets bigger.

Nichrome is used for glows-red heating elements because it's stable at high temps. In a speaker emulator, if you used the typical thickness of nichrome in a hair dryer, it would not be changing temp nearly as much as in the hair dryer it came from. These devices tend to be about 1kW on high setting, that being about all you can reliably get out of a 15A socket.

Hmmm. Here's a thought. For 120Vrms and 8 ohms, the power is about 120*120/8 = 1800W. So if your amp can put out 1kW+, a hair dryer or toaster makes a modestly good dummy load as is.

Thanks for your answer. Sounds as if resistance constancy isn't much of a concern if it's actually nichrome.

[rjb]

Here's a question they used to try to spring on us:

Advanced "trick" question:
Twelve 1-ohm resistors are configured so that each resistor is the edge of a cube.
What is the resistance between diagonally opposite corners, i.e. corners that are points on a line that passes through the cube's center?

Trick: Inject an imaginary 1 amp current at one corner and calculate the voltage drops across each resistor- noting that due to symmetry, the current will split equally at each node.

-rb

[R.G.]

Oh, right. Otherwise, we would need to know the battery voltage... which was omitted on PURPOSE!
Very sneaky. Very sneaky indeed.

It was a dead giveaway!

The "H" point impedance can be anything between a short circuit and an open circuit with no effect whatsoever on the other elements. The logic behind this is a special case of the logic for all bridge-type sensing circuits.

[rjb]

The "H" point impedance can be anything between a short circuit and an open circuit with no effect whatsoever on the other elements. The logic behind this is a special case of the logic for all bridge-type sensing circuits.

Yea, but... you never stated the tolerance of the 8-ohm resistors.

-rb