Horseshoe pickups: what do they do that's "different"?

[rjb]

This is a provocative suggestion.

I sure didn't mean it to be provocative. But apparently, it is.
Hoowee, calm down, guys! I think you-all have just had a few misunderstandings.

And, although informative, I don't see what most of the discussion has to do with the original question:
What makes horseshoe pickups uniquely suited for slide guitar?

EDIT: Here are some drawings of the pickup configuration under discussion.
(Source: Stolen from a paper by Hartley Peavey)

[Mike Sulzer]

What makes horseshoe pickups uniquely suited for slide guitar?

I guess a large part of it is that they do sound different, and they are what was originally used. This tends to make them sound right. Perhaps somebody could make something "better" to somebody's ear, but if you have been listening for many years, you probably think, with good reason, that you know what is right.

The near constancy of the field and thus low string pull could have a lot to do with it, but maybe there are other factors as well. How about the type of iron the pole pieces? What about eddy currents in the cobalt steel magnet? Magnetic stuff is in general really complicated for multiple reasons.

[Joe Gwinn]

So "side pull" is in the direction of the change in magnetic field, whether that be side wise or vertical in the usual use of these terms with pickup.

Yes. Specifically, the gradient. The force is directed towards increasing magnetic flux.

[ScottA]

OK, I thought you meant just the flux from the permanent magnet.

Yes, magnetizung the string. Now it is possible to say that without starting an argument with a certain former moderator who insisted that it did not happen.

No, I meant the flux from the vibrating string. I guess I was not explicit.

I actually did this quick and dirty experiment last night when I saw this thread.

I placed a Zexcoil with no magnet (but everything else: coils, pole pieces, etc.) above the strings on a guitar with a finished Zexcoil installed and toggled between the two pickups.

The one above the strings (without a magnet) was just as loud as the installed one (with the magnets) at about the same distance from the strings.

[Mike Sulzer]

Just as it should be, except in situations when the permanent magnet is saturating, or nearly so, the cores, or a few other very unlikely scenarios.

No, I meant the flux from the vibrating string. I guess I was not explicit.

I actually did this quick and dirty experiment last night when I saw this thread.

I placed a Zexcoil with no magnet (but everything else: coils, pole pieces, etc.) above the strings on a guitar with a finished Zexcoil installed and toggled between the two pickups.

The one above the strings (without a magnet) was just as loud as the installed one (with the magnets) at about the same distance from the strings.

[rjb]

I guess a large part of it is that they do sound different, and they are what was originally used. This tends to make them sound right....
The near constancy of the field and thus low string pull could have a lot to do with it...

Do we agree, as bbsailor asserted in Post3, that this configuration (at least theoretically) produces a more symmetrical output, and thus a closer representation of the string's vibration, than conventional "side-pulling" (a new term) pickups?

Can someone suggest or identify an electromagnetic pickup which produces a more faithful translation of string vibration to electrical signal?

---

PS:

I do realize from Lenz's Law that the signal generated by a magnetic pickup is out of phase with the string's vibration.

Ex.) For the sake of simplification, pretend the string moves "up and down" in simple sinusoidal fashion.
The string's velocity mimics that of a child's swing- it slows to zero and changes direction at the "peaks"; and attains maximum velocity at the "middle".

So, in a "side pull" pickup, the induced voltage is zero when the string's velocity is zero- at the top & bottom of it's travel (at the points farthest and nearest to the pole pieces). I reason maximum voltage is attained at a point near the string's at-rest position, but closer to the pole piece side- where the product of the string's velocity and magnetic field are greatest. The positive and negative peak voltages should be the same magnitude- because they occur when the string passes through the same point in space, from opposite directions.

I think this analysis predicts a distortion in the signal's "width" (resulting in a lop-sided shape with mirror-imaged top and bottom), rather than a distortion in "height" (different positive & negative magnitudes). But, in a general sense, distortion is distortion.

[bbsailor]

Do we agree, as bbsailor asserted in Post3, that this configuration (at least theoretically) produces a more symmetrical output, and thus a closer representation of the string's vibration, than conventional "side-pulling" (a new term) pickups?

Can someone suggest or identify an electromagnetic pickup which produces a more faithful translation of string vibration to electrical signal?

rjb and all

Back in 2010 I started this "over and under" pickup design thread to introduce a discussion about the "side pulling" effect of traditional pickup designs. See this: http://music-electronics-forum.com/t21125/ for an interesting discussion.

Joseph Rogowski

[Mark Hammer]

Thanks for bringing that up again, Joseph. Much appreciated.

If I can ask another innocent question: When a string passes through such an over-and-under pickup, is it, or would it theoretically be, necessary for the distance between the string and the field above and field below to be equidistant? (I gather this assumes adjustment for the strength of the respective upper and lower fields.) For instance, if the upper part of the "horseshoe" was weaker, whether by virtue of the material itself, or simply the distance, would the advantages be eliminated?

[Mike Sulzer]

Do we agree, as bbsailor asserted in Post3, that this configuration (at least theoretically) produces a more symmetrical output, and thus a closer representation of the string's vibration, than conventional "side-pulling" (a new term) pickups?

The effect should not be considered significant at the intensity of field usually used unless it is shown to be by careful measurement. Remember, any wave form containing even harmonics could be asymmetrical.

[Joe Gwinn]

I do realize from Lenz's Law that the signal generated by a magnetic pickup is out of phase with the string's vibration.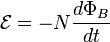

Well, to be pedantic, this is not Lenz's Law, it's Faraday's Law of Induction. Translated into English, the equation says that the voltage in a single turn is proportional to the negative of the time rate of change of flux (lines, not Gauss) passing through that single turn. Lenz's contribution to this equation is the negative sign.

[rjb]

Well, to be pedantic, this is not Lenz's Law, it's Faraday's Law of Induction.

Oops. Confession: Back when I attended engineering school during a previous lifetime, I was a lousy student.

Let's try this:

For a tightly wound coil of wire, composed of N identical turns, each with the same Φ_B, Faraday's law of induction states that

where N is the number of turns of wire and Φ_B is the magnetic flux through a single loop.

Sulzer's Law of Magnetic Pickups states "The permanent magnet magnetizes the string, and the string's moving field induces the voltage across the coil". (I hope that's close enough for MEF.)

Now, combining Faraday's Law of Induction with Sulzer's Law of Magnetic Pickups, does it follow that the induced voltage is zero when the string is at its furthest excursion from its resting point- that is, at the instant when the string changes directions and has zero velocity?

[Mike Sulzer]

does it follow that the induced voltage is zero when the string is at its furthest excursion from its resting point- that is, at the instant when the string changes directions and has zero velocity?

Are you thinking that your proposition implies that the changes in permanent B field with distance from the pickup have less effect than expected because the voltage produced is zero at the extremes and maximum in between, both when the string is headed towards and away from the pickup?

[Joe Gwinn]

Now, combining Faraday's Law of Induction with Sulzer's Law of Magnetic Pickups, does it follow that the induced voltage is zero when the string is at its furthest excursion from its resting point - that is, at the instant when the string changes directions and has zero velocity?

Yes. If the string is stationary, the flux is not changing, so no voltage at the instant of standstill. This is seen as a zero crossing in a voltage versus time plot.

[Joe Gwinn]

Let's try this:

Sulzer's Law of Magnetic Pickups states "The permanent magnet magnetizes the string, and the string's moving field induces the voltage in the coil". (I hope that's close enough for MEF.)

While is is a perfectly valid way to view things, there are other valid ways as well. These are all members of the class Variable-Reluctance Sensor, which share the fact that the various coils and magnetized components move so slowly with respect to one another that one can treat such systems as if the magnetic flux were constant while figuring out flux values, yielding a function of flux versus position of say a string. This is an application of the quasi-static approximation. Knowing the motion of the string, one can compute the flux versus time, which feeds directly into the law of induction to yield the voltage versus time.

Now to be pedantic (again), the fact that we have significant eddy-current effects means that pickups are not totally in the quasi-static regime, but it's close enough to be useful in practice.

[Mike Sulzer]

While is is a perfectly valid way to view things, there are other valid ways as well. These are all members of the class Variable-Reluctance Sensor, ...

Not only is it perfectly valid, but it is essentially fundamental, at least at the level of classical physics, and thus is to be preferred, unless there is some real advantage to the variable reluctance view. There is not in the case of a pickup.

The variable reluctance view has strength in simplicity when an analogy with electrical circuits (resistors, batteries, wires) is valid. The high permeability portions of a magnetic circuit are like wires, and small gaps are like resistors. There is a simple equation for the reluctance (resistance of the "resistor") because the problem can be reduced in dimensionality (edge effects are small, etc.) when the gap is small.

Pickups have a short (usually) high permeability pole piece, a very small high permeability bit of string and a huge air space. The "flow" of flux is limited by this space. Solving for its multi dimensional "reluctance" requires solving a three dimensional partial differential equation, the same equation that would have to be solved in the electrical case where we have three dimensional flow (current density) driven by an electric field which must be solved for in a self-consistent way. The problems are the same, and so if one is not simple, then neither is the other.

The pickup is much simpler when analyzed in a two step process where an applied field magnetizes a bit of string. Even determining the magnetization of the string is not such a simple problem, but because it is small, you can approximate and even get an answer with a two dimensional solver such as FEMM. Once that is done, you use linearity to eliminate the permanent field from the problem and look at the flux through the coil for difference positions of the vibrating string. You can even vary the magnetization of the string as a function of position (the effect that Joseph mentioned) if you like.