Question regarding the tone knob's relationship with the resonant peak

[Antigua]

Hello! I learned on another (guitar) forum that when you turn the tone knob down, the resonant peak doesn't actually become a smaller value until the tone control is at or close to zero. While the knob is at a higher setting, between five and ten, the resonant peak is still about the same as if the knob were at ten, but the peak amplitude, or Q factor, just becomes lower. Here's a graph someone provided:



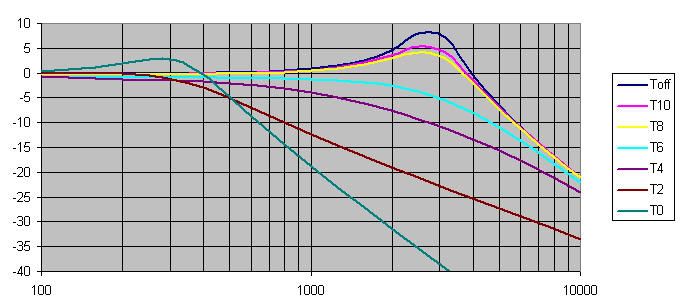
As you can see, the movement of the peak isn't a straight line from high peak to low peak, but is instead a "swoosh" where the amplitude drops as the tone control is rolled close to zero, but once it hit's at zero, the amplitude makes a sudden come back, but at a lower resonant peak.

I understand why the capacitor by itself decreases the peak resonance, as it effects the LCR equation to arrive at that end result, but what I don't understand is why the tone knob's dial's relationship to the resonant peak and amplitude isn't more linear. What causes the Q / peak amplitude to drop in the beginning (dial between 5 and 10), and then suddenly pick back up with the lower resonant peak towards the end (dial at/near zero)?

[pdf64]

I think that in the ~5-10 range, the tone control is just varying the load on the pickup; the cap could be replaced by a shorting link and it works the same.
At '0' the cap forms a resonant circuit with the pickup; as the control is turned up from 0, the Q and magnitude of the resonant circuit are reduced.

[charrich56]

Yes, pdf64, I think that's a good explanation. Just to add a little bit, the higher peak resonance between 2 and 3 KHz that you see in that chart at high tone pot settings is the self-resonance of the inductance and capacitance of the pickup itself, along with the cable capacitance in a passive pickup. The tone cap is much larger in capacitance than the stray capacitance of the pickup and cable, and interacts with the pickup inductance at low tone pot settings, producing a much lower resonance.

In one chart, this explains the incredible distaste that many, many guitarists have for "normal" tone controls.

[Antigua]

I think that in the ~5-10 range, the tone control is just varying the load on the pickup; the cap could be replaced by a shorting link and it works the same.
At '0' the cap forms a resonant circuit with the pickup; as the control is turned up from 0, the Q and magnitude of the resonant circuit are reduced.

That's a good summary, but why is it that between five and ten the cap could be replaced with a pieces of wire and it wouldn't matter? If load increases as you turn down the tone dial, why does the Q factor rebound at zero? I don't understand why I'm seeing a big Nike-logo-like curve where logically I'd expect more of a quarter pipe.

[Mike Sulzer]

That's a good summary, but why is it that between five and ten the cap could be replaced with a pieces of wire and it wouldn't matter?

The resistance of the pot is large compared to the magnitude of the impedance of the tone cap at frequencies near the coil-cable resonance. Therefore the effect of shorting out the cap would be small. The impedance of the pickup is a lot lower at lower frequencies, so nothing much happens there until the larger tone cap begins to play a role.

If load increases as you turn down the tone dial, why does the Q factor rebound at zero? I don't understand why I'm seeing a big Nike-logo-like curve where logically I'd expect more of a quarter pipe.

The series resistance of the pot damps the resonance that would otherwise occur with the tone cap until the resistance is small enough.

[J M Fahey]

why does the Q factor rebound at zero?

See it this way:

* with tone "OFF" the main resonance is between pickup inductance and self plus cable capacitance, which is small, 100's of pF, the resonant peak frequency is highest (bright/biting/shimmery sound) and Q is *relatively* high, resonance is damped by pickup DC resistance, the guys at the pickup section are the experts but in general we are talking, say, from 1500 to 5000 or 6000 ohms in normal pickups (am I right guys?)
The tone cap is still in parallel with the pickup and resonates, but at the far end of a huge resistor, the tone pot, so its effect is nil.

* With tone full ON , same as before, pickup + cap resonates, relatively high Q, significant resistance id pickup DCR.
Resonant frequency will be way lower, bacause tone cap is *huge* compared to all others

* with tone pot set at intermediate points: tone cap, being way higher, swamps effect of other caps, BUT it's connected through a large series resistor (the pot section enabled) so Q is horrible, way below 1, and response is similar to a plain treble cut.

Personally I'd ditch the crude "tone" control and install a roary switch to select between many caps, best of both worlds.

*

[Antigua]

Thanks for the explanations, things are getting clearer, but why isn't the load super high when the tone control is at zero, but yet the load is increased all the same when the tone pot is at 5? If the tone capacitor in series doesn't cause added load with the tone knob at zero, shouldn't it not cause added load with the tone knob 5?

[J M Fahey]

The tone capacitor *is* a load for the pickup, no doubt, but the pickup is not resistive but inductive, so they have a resonant frequency which may be (and is) higher in peak value than plain driving a 1 M resistor.

FWIW a seldom noticed trick in reverb tanks is to add a small cap in parallel with the recovery input; most think it's just for RF filtering but I found iot's tuned to, say, 3 or 4 kHz, and significantly brightens reverb response.

Another case of "hidden in plain sight" .

[Mike Sulzer]

See it this way:

* with tone "OFF" the main resonance is between pickup inductance and self plus cable capacitance, which is small, 100's of pF, the resonant peak frequency is highest (bright/biting/shimmery sound) and Q is *relatively* high, resonance is damped by pickup DC resistance, the guys at the pickup section are the experts but in general we are talking, say, from 1500 to 5000 or 6000 ohms in normal pickups (am I right guys?)
The tone cap is still in parallel with the pickup and resonates, but at the far end of a huge resistor, the tone pot, so its effect is nil.

* With tone full ON , same as before, pickup + cap resonates, relatively high Q, significant resistance id pickup DCR.
Resonant frequency will be way lower, bacause tone cap is *huge* compared to all others

* with tone pot set at intermediate points: tone cap, being way higher, swamps effect of other caps, BUT it's connected through a large series resistor (the pot section enabled) so Q is horrible, way below 1, and response is similar to a plain treble cut.

Personally I'd ditch the crude "tone" control and install a roary switch to select between many caps, best of both worlds.

*

The series resistance is only part of the damping. Both tone (through the tone cap) and volume pot have a significant effect. In a pickup using steel cores such as most humbuckers the eddy currents can be the biggest factor in the damping.

I agree, the rotary switch is the way to go. I prefer to drop the impedance about 10 or 20 times (fewer turns) to effectively eliminate the effect of the cable capacitance, adjusting the caps on the switch as needed, use a 25 K vol pot, and then run to an external low noise FET preamp to make the SNR equal or better than with a high output pickup into a 12AX7.

[pdf64]

After two+ decades of ignoring it, over the past few years I've really got to appreciate the regular guitar tone control, especially with the '50s' style 'tone after volume' arrangement; a twist of the volume can take me from clean&bright to crunchy to thick overdrive.
The key for me is to set amp controls for bright usable tones from the neck / middle pickup, then it all falls into place and the tone control/s become useful.

[J M Fahey]

Yes, cut only controls take on a new life when the peaking/boosting takes place outside, well beyond what's ususlly needed.
Under that scenario, cut only is equivalent, in practical use, to cut and boost.

I remember Loooong ago (please, don't do the Math ) reading British music magazines, way before Guitar Player if you can imagine that, where I absorbed and reprocessed every tiny bit of data to pull useful info.
Just the name discloses the era: "Beat Instrumental" .
As a free sample of the state of common knowledge and technology way back then, among other firsts (I can't believe that was just "last month news" buried among 1000 other small News, without any special importance) I read there about coming shows by a local band called Deep Purple, where they would demonstrate live some amps called Marshall, full page ads of Black Sabbath using tons of "power simulators" which were Laney 100W power amps, driving 4x12" square (guitar/bass) or column (PA) cabinets .
A head and 9 or 10 "simulators" each musician, voice was certainly all mids, distorted and impossible to understand.
I mention this to set the background, because one day a small note in , say, page 24 or 36 or some other unimportant place mentioned that ELP (Emerson Lake and Palmer) had played a cinema in a small British town and "just for fun" hooked one PA head (probably tube 100W) to the cinema speakers, including a Vitavox horn.
They were *crushed* by the "crystal clear sound" and from then on carried Cinema speaker systems everywhere, no matter the inconvenience.

In that abysmal sound quality world, much discussion was generated about the Precision Bass sound, "which could go from bell like piano sound to deep rumbling bass at the turn of a single pot".

And much analysis (without clear conclusions) was applied to the ".1 uF ceramic capacitor" and its seemingly magic range.

Truth is, standard British Bass amps way back then were "a Marshall" (or a very similar one by another maker) driving tons of Celestion/Fane/Goodmans 12" speakers.

There was excess brightness all over the place (roundwound strings were also becoming known) , so in those stages and cavernous halls , a simple treble cut control *did* provide all necessary range of adjustment and then some.

FWIW some friends travelled to England and bought a full set (including a Mellotron) and for the Bass brought a Marshall with 4x15" speakers.

Now we have Bass!!l you woukd think .

Not at all; the 4 x 15" speakers were housed in a rectangular *thin* cabinet (imagine a shallow cupboard) , and any Bass you plugged there was either unbearably shrill or dull, pick one, but no real Bass whatsoever.
I guess Bass would appear anyway courtesy of the booming Basketball Stadium or untreated cement or brick walls of the hall they were playing in.
Butb that Marshall was so tinny sounding that one of them spent a small fortune (what a car would cost) , travelled to NY and brought back an Ampeg V4B with a fridge sized 2 x 15" folded horn.

So yes, simple tone controls were more useful than they seem, because (I guess) amps were developed and equalized with them in mind.

[Antigua]

I'm trying to understand this, answer true or false: when the cap is directly in parallel with the pickup, they can combine to alter the coil's resonance, but when the capacitor is placed behind (in series with) sufficient resistance (apparently anything north of 20 k ohms, give or take), the capacitor and pickup are unable to combine in such a way that alters the coil resonance.

And it's also true that when the tone knob is at zero, the pickup is under a high load? It's confusing that a capacitor can be though of as a "piece of wire" since current never actually passes though a capacitor, is just collects at the opposing plates on either side of the dielectric, so the manner in which the cap is able to impose added load in parallel with the pickup is sort of a mystery in that respect.

[eschertron]

I'm trying to understand this, answer true or false: when the cap is directly in parallel with the pickup, they can combine to alter the coil's resonance, but when the capacitor is placed behind (in series with) sufficient resistance (apparently anything north of 20 k ohms, give or take), the capacitor and pickup are unable to combine in such a way that alters the coil resonance.

I guessing that a vector graph, showing the reactance of the pot and cap in series, would reveal that the cap's effects are swamped by the pot. The reactance of that combination doesn't add linearly with the coil's impedance. Someone better versed in complex math might use the words that make it all plain...

And it's also true that when the tone knob is at zero, the pickup is under a high load? It's confusing that a capacitor can be though of as a "piece of wire" since current never actually passes though a capacitor, is just collects at the opposing plates on either side of the dielectric, so the manner in which the cap is able to impose added load in parallel with the pickup is sort of a mystery in that respect.

At audio frequencies - frequencies where the cap's impedance looks small - the cap is effectively a piece of wire. The electrons don't travel through the dielectric, but the electrons are not restricted from bouncing in and out of the cap as if they were actually going somewhere. Limited by whatever time constant - RC or LC ? - has the greatest effect.

[Antigua]

Thanks for the capacitor explanation, that makes sense.

They say math is just a way of describing the relationship about things, and I've seen some YouTube videos that show with visual aids how the electrons gather on the plates of dielectrics, and even how adding a resistor in series impedes the coming and going of electrons to the cap, and for me and I think a lot of other people, that visual approach is a lot easier to follow than the math, which I think tends to tell you something is happening, but not why. I'm not sure why capacitors behave differently at different frequencies though, that's harder to visualize in terms of electrons coming and going.

[loudthud]

A capacitor can pass AC current. I worked on a project where two .047uF 600V Sprague 716P caps were in series with a large 8 turn hoop of #14 romex wire. At 166KHz the whole thing resonated and the current was adjusted to 10 Amps peak to peak. The Voltage across each cap was a couple of hundred Volts peak to peak. The whole thing was driven by a bridge amp with a single 16V rail. This thing would melt a Polyester film cap in seconds.

The Q of a guitar pickup isn't very high to begin with. Any resistance between the pickup and a capacitance will lower the Q to the point where there is almost no peaking. When the pickup is resonating with the tone cap, a resistance of 10K to 20K will lower the Q to that point. So you don't get a peak until the tone pot is all the way down. When the tone pot is all the way up, it's resistance is high enough that the pickup can resonate with the cable capacitance. The tone cap is a low impedance at the higher resonant frequency and it is isolated by the resistance of the tone pot. If you short the tone cap, it doesn't affect the resonance much. If you back off on the Volume control, the resistance between the pickup and the cable kill that resonance but the pickup still has enough parasitic capacitance to self resonate at a somewhat higher frequency.