Output Stage & calculating halfboost freq. can you doublecheck my results?

[Mike Sulzer]

(...I'm afraid to even ask)

So, when you refer to the square root term, are you referring to this entire expression
[ATTACH=CONFIG]47677[/ATTACH]
where as using the figures I was going by, I got 1/(2πRkCk)*sqrt(1.05346294) = 1/(2πRkCk)*1.026383427388

you would simplify it to say 1/(2πRkCk)*sqrt(3) = 1/(2πRkCk)*1.7320508075688772
??
go easy on me.

Yes, but I think you used mu = 19? It needs to be much higher. However, I think it is not high enough for my approximation to work very well.

[Mike Sulzer]

Hello Mike,

you are right, the -6dB or half-gain-frequency differs from the -3dB frequency by a factor of (3)^0.5. But the -6dB frequency of an ideal first order high pass filter must be lower than the -3dB frequency, whereas the square root term in the formula from the article can only increase the frequency value.
For the ECC83 example in the paper the square root term yields a factor of 1.17.
I don't think the formula in the paper can be used for pentodes also. Pentodes do have higher µ values as well as higher ra values, which would partly compensate in the formula. µ is actually a theoretical number, meaning the intrinsic open-loop-voltage-gain. It is not typically found in pentode specs as it strongly depends on operating conditions. It is certainly much higher than the value of 17 given in Post 1.
With all these uncertainties I would go by the simple -3dB formula, which at least gets you in the ballpark, even if the frequency may be a little too low.
If it has to be precise, nothing beats a measurement of the stage's frequency response.

Yes, mu*Rk is not high enough compared ra + Ra for the approximation I proposed to work. So if mu is condition dependent and you do not have the right number (or even worse,there is no right number because it is not constant as used in the circuit), then there is no way to compute the half boost frequency as accurately for pentodes as there is for triodes.

[SoulFetish]

The Rk is in K ohms, so for example for 470 ohms enter 0.47. I don't see any error messages.

wait... you mean I have to put the little dot thingy before the numbers???

That's what I been trying to tell you, man. When I did that, the strangest error message pops up on my screen.



Which is weird, 'cause my name's not Dave.
But I just tried it again on the link you posted and it seemed to work fine. You must have fixed it.
But here is the error I got. I may have been using the html file you posted when you were working on it.

[Helmholtz]

True. The slider has to have an upper limit. I've changed it to 500.

Thanks, nickb!

To give an example for power pentodes: My EL84 datasheet specifies ra=40k, transconductance gm=10mA/V. Using Barkhausen's equation for triodes (might actually require some minor modification for pentodes, who knows?) I get µ=ra*gm=400.

I still would like to warn against taking tube parameters as precise constants. While the µ of an ECC83 is relatively constant (high quality tubes having a tolerance of +/- 10%, when new), ra varies over more than a factor of 2 with anode current. In addition there is a dependency of ra on anode voltage in the range of 15%.

Along with the tolerances of the electrolytics (loosing capacity over lifetime) the half-boost-frequency cannot be precisely predicted/designed.

[nickb]

wait... you mean I have to put the little dot thingy before the numbers???

That's what I been trying to tell you, man. When I did that, the strangest error message pops up on my screen.



Which is weird, 'cause my name's not Dave.
But I just tried it again on the link you posted and it seemed to work fine. You must have fixed it.
But here is the error I got. I may have been using the html file you posted when you were working on it.

[ATTACH=CONFIG]47688[/ATTACH]

The link I gave doesn't look like that...

Dave (), you were looking at a (much, much) earlier version that used the -3dB frequency. I'm guessing you downloaded it some time ago? If Rk is too small then the difference between max and min gains will be less that 3db in which case the error message is correct, no solution exists.

Moving on, I wonder about if perhaps you have considered that the time constants might be of sonic significance. What we have been talking about is all pure linear operation. Even a class A stage will lead to some charging of the cathode cap so changing the bias. A class AB push pull much more so. This has sonic implications that will affect your choice of time constant and might lead you to choose something in the < 10 Hz range.

[SoulFetish]

Along with the tolerances of the electrolytics (loosing capacity over lifetime) the half-boost-frequency cannot be precisely predicted/designed.

This is one of the reason's I don't use them if I can help it.

[Mike Sulzer]

Back to the calculation in the first post. I implemented the equation in Radiation... (eq.2, page 484) in Python, and verified the result against nick's online calculator. I then did the original calculation in the first post and got 36Hz. But this is meaningless because the difference between the minimum and maximum gain is a fraction of a db. This is because a tube with 38K ra and a hypothesized mu of 19 has a very low transconductance, and thus a higher than normal impedance looking into the cathode (2000 ohms). As a result the 220 ohm Rk does nothing much.

So I did it with higher mu, using 350, 400, and 450, to check how much the half boost frequency shifts with change in mu. The results are shown in the attachment.

[SoulFetish]

Great work as alway, Mike!
The Graph seems to indicate a pretty linear relationship between stage mu halfboost frequency. Could we assume that a Mu of 300 would yeald a halfboost of 59Hz and a Mu of 500 - one of 79Hz?

[Helmholtz]

Can you double check my results?
I'm calculating the halfboost frequency for a given cathode bypass capacitor value in an output stage. Most of the discussions seem to center around implementation in a preamp stage. In order to achieve accurate results, I'm using this formula:

*
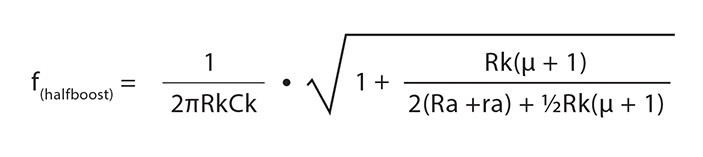
The formula was found in this short article:
http://valvewizard.co.uk/ChoosingBypassCaps.pdf
Here is the datasheet for an EL84:
[ATTACH]47627[/ATTACH]
*
the parameters for a pair of EL84s operating in a class AB push-pull output stage are as follows:
10k p-p load impedance
220Ω Rk(per tube)
20µF Ck(per Rk)
internal resistance ≈ 38k
µ = 19

solving for f during class B operation I came up with f_(halfboost) ≈ 37Hz (37.125908162)
Is this correct?

The amplification factor of 19 from the attached datasheet is not the µ you want. It is actually the µg2g1, which is the amplification factor of the second grid. The real µ of the EL84 has to be much higher. It is not specified in the datasheet, but µ around 400 should be a good starting point.

My resumee from the paper is, that the half-boost frequency is always somewhat higher than the -3dB frequency. This is because the result from the root term is always larger than one. Its maximum value according to the paper is square root of 3 (=1,73). This is also logical, as the very low frequency gain does not drop to zero as in an ideal first order high pass filter.
Consequently the half-boost frequency can vary between 36Hz and 63Hz max for Rk=220 Ohm and Ck=20µF.

Electrolytics have wide tolerances, but are the only practical choice for cap values above 10...15µ. They are only available in stepped standard values.
Rk defines bias (idle current) and thus cannot be varied freely.
The µ-value is often not very well known and ra varies strongly with bias current.
In output stages Ra is not constant, because the speaker impedance varies with frequency. At the speaker resonance (near 100Hz) the impedance of an 8 Ohm speaker can rise up to 100 Ohms.
Ra also varies between the low power class A region and the high power class B region in class AB amplifiers.
The half-boost frequency will be influenced by an outer feedback loop.

Thus, most of the parameters needed are not very well defined.

Nevertheless, your result of f=37Hz may be somewhat too low but is certainly in the ballpark.

Here is some information on µ:
Amplification and Valve Characteristics

[Mike Sulzer]

Great work as alway, Mike!
The Graph seems to indicate a pretty linear relationship between stage mu halfboost frequency. Could we assume that a Mu of 300 would yeald a halfboost of 59Hz and a Mu of 500 - one of 79Hz?

The apparent approximately linear variation cannot continue; the half boost frequency reaches a limit.

However, I think varying mu in this way is not realistic. mu = gm*ra. An EL34 has a gm of 11 mA/V when connected as a pentode with an ra of 15K. Connected as a triode, the gm is 11.5 mA/V and ra is 910 ohms. The difference between the mu of a triode and a pentode is almost entirely due to variation of ra through the relationship mu = gm*ra. This is in agreement with the physics because the screen grid causes electrons to accelerate electrons to the plate even when the plate voltage is not so high.

So let's vary ra and thus gm through this relationship and put these parameters in the equation. The results are attached, and there is very little variation in the half boost frequency. Both ra and mu are varying because ra is varied directly and mu varies through the relationship mu = gm*ra. gm is held constant.

[SoulFetish]

The apparent approximately linear variation cannot continue; the half boost frequency reaches a limit.

However, I think varying mu in this way is not realistic. mu = gm*ra. An EL34 has a gm of 11 mA/V when connected as a pentode with an ra of 15K. Connected as a triode, the gm is 11.5 mA/V and ra is 910 ohms. The difference between the mu of a triode and a pentode is almost entirely due to variation of ra through the relationship mu = gm*ra. This is in agreement with the physics because the screen grid causes electrons to accelerate electrons to the plate even when the plate voltage is not so high.

Thanks. Got it.
To all how responded; this has been good conversation and I was able learn something from each of you. As always, I really appreciate it.

[Helmholtz]

I found this in an old physics textbook (Methods of Experimental Physics, Marton 1964):



(Not sure, if I could upload the .png correctly)

It does not give the half-boost frequency, but shows that only the lower corner frequency f1 is determined by the Rk*Ck value, while the upper corner frequency f2 shifts and rises with the gain ratio G1/G2. I wasn't aware of this. Very interesting.

BTW, it is not easy to spot the half-boost point on a log (dB) gain scale plot without some calculation. In most cases this point will not lie in the middle between the levels.

[Malcolm Irving]

The formulae based on G1 and G2 seem very useful, as we can easily calculate G1 as the fully-bypassed gain and G2 as the unbypassed gain, then the calculated f1 and f2 probably tell us all we need to know about bass cut. (Or you can use this for treble-boost by having higher values of f1 and f2.)

[Mike Sulzer]

BTW, it is not easy to spot the half-boost point on a log (dB) gain scale plot without some calculation. In most cases this point will not lie in the middle between the levels.

That is why my plots above are on a linear scale, with the half boost point solved for and marked on the plot.

f1 and f2 appear to be definitions. For example, the time constant at the cathode depends on R2, C, and the impedance looking into the cathode. Since the ratio G1/G2 is usually not very large, f2 cannot be interpreted as a 3db point either.

[Malcolm Irving]

Does the 1964 textbook give any analysis to support the formulae?
In Merlin’s latest book ‘Designing High-Fidelity Tube Preamps’ he writes about the system having a pole at f = 1 / ( 2.pi.Ck (Rk || rk) )
and a zero at f = 1 / ( 2.pi.Ck.Rk ). But we have to be wary of inferring 3dB points from that, as poles and zeros which are close together disturb the position of the 3dB points.